설명
검색이란
- 저장되어 있는 자료 중에서 원하는 항목을 찾는 작업
- 목적하는 탐색 키를 가진 항목을 찾는 것
- 탐색 키(search key): 자료를 구별하여 인식할 수 있는 키
- 검색의 종류
- 순차 검색 (sequentail search)
- 이진 검색 (binary search)
순차 검색 (Sequential Search)
- 일렬로 되어 있는 자료를 순서대로 검색하는 방법
- 가장 간단하고 직관적인 검색 방법
- 배열이나 연결 리스트 등 순차구조로 구현된 자료구조에서 원하는 항목을 찾을 때 유용함
- 알고리즘이 단순하여 구현이 쉽지만, 검색 대상의 수가 많은 경우에는 수행시간이 급격히 증가하여 비효율적
- 2가지 경우
- 정렬되어 있지 않은 경우
- 정렬되어 있는 경우
정렬되어 있지 않은 경우
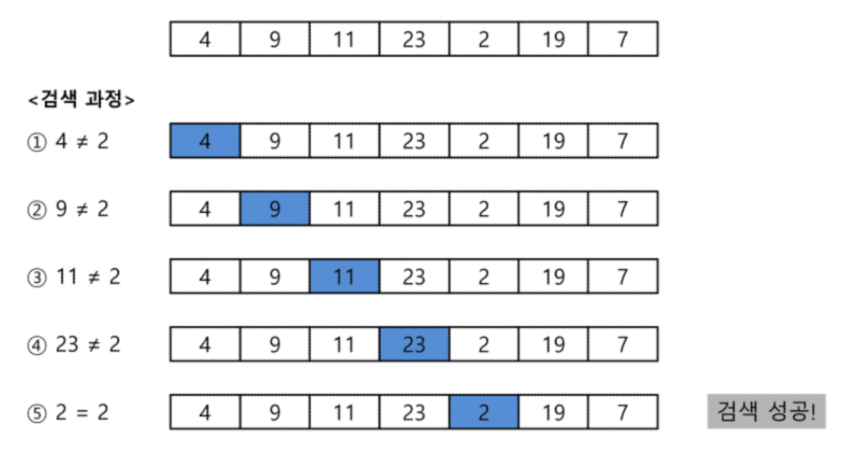
- 검색 과정
- 첫 번째 원소부터 순서대로 검색 대상과 키 값이 같은 원소가 있는지 비교하며 탐색
- 키 값이 동일한 원소를 찾으면 그 원소의 인덱스를 반환
- 자료조의 마지막에 이를 때까지 검색 대상을 찾지 못하면 검색 실패
- 찾고자 하는 원소의 순서에 따라 비교횟수가 결정
- 첫 번째 원소를 찾을 때는 1번 비교, 두 번째 원소를 찾을 때는 2번 비교
- 정렬되지 않은 자료에서의 순차 검색의 평균 비교 횟수
= (1/n) * (1+2+3+...+n) = (n+1)/2
- 시간 복잡도: O(n)

- 예시 코드
# 정렬되어 있지 않은 경우
arr = [4, 9, 11, 23, 19, 7]
def sequentialSearch(_list, key):
for i in range(len(_list)):
if key == arr[i]:
return i
break
else:
return False
print(sequentialSearch(arr, 2)) # => False
print(sequentialSearch(arr, 19)) # => 4
정렬되어 있는 경우
- 검색 과정
- 자료가 오름차순으로 정렬된 상태에서 검색을 실시한다고 가정
- 자료를 순차적으로 검색하면서 키 값을 비교
- 원소의 키 값이 검색 대상의 키 값보다 크면 찾는 원소가 없다는 것이므로 더 이상 검색하지 않고 종료
- 찾고자 하는 원소의 순서에 따라 비교회수가 결정됨
- 정렬이 되어있으므로, 검색 실패를 반환하는 경우 평균 비교 회수가 반으로 줄어듦
- 시간 복잡도: O(n)


- 예시
# 정렬되어 있는 경우
arr_2 = [4, 7, 9, 11, 19, 23]
def sequentialSearch2(_list, key):
for i in range(len(_list)):
if key == arr_2[i]:
return i
break
elif key < arr_2[i]:
return f"{i+1}번째 원소까지 검색했지만 없음", False
break
print(sequentialSearch2(arr_2, 10)) # => (3번째 원소까지 검색했지만 없음, False)
print(sequentialSearch2(arr_2, 9)) # => 2
이진 검색 (Binary Search)
- 자료의 가운데에 있는 항목의 키 값과 비교하여 다음 검색의 위치를 결정하고 검색을 계속 진행하는 방법
- 목적 키를 찾을 때까지 이진 검색을 순환적으로 반복 수행함으로써 검색 범위를 반으로 줄여가면서 보다 빠르게 검색을 수행
- 이진 검색을 하기 위해서는 자료가 정렬되어 있어야 함
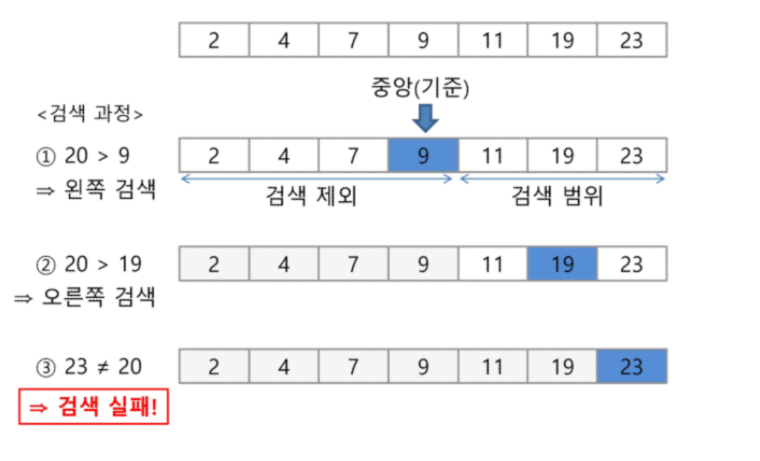
- 검색 과정
- 자료의 중앙에 있는 원소를 선택
- 중앙 원소의 값과 찾고자 하는 목표 값을 비교
- 목표 값이 중앙 원소의 값보다 작다면
- 자료의 왼쪽 반에 대해서 새로 검색을 수행
- 목표 값이 중앙 원소의 값보다 크다면
- 자료의 오른쪽 반에 대해서 새로 검색을 수행
- 찾고자 하는 값을 찾을 때까지 위의 과정을 반복
- 시간 복잡도: O(log n)

- 예시
def binarySearch(_list, key):
start = 0
end = len(_list) - 1
while start <= end:
middle = int((start + end) // 2)
if _list[middle] == key: # 검색 성공
return f"{middle}번째 인덱스 값"
elif _list[middle] > key:
end = middle - 1
else:
start = middle + 1
return False, "검색 실패"
arr = [2, 4, 7, 9, 11, 19, 23]
print(binarySearch(arr, 7)) # => 2번째 인덱스 값
print(binarySearch(arr, 20)) # => (False, '검색 실패')'Algorithm' 카테고리의 다른 글
| 패턴 매칭에 사용되는 알고리즘 (0) | 2021.02.19 |
|---|---|
| Selection Algorithm & Selection Sort (셀렉션 알고리즘, 선택 정렬) (0) | 2021.02.16 |
| Subset & Bitwise operator (부분집합과 비트 연산) (0) | 2021.02.15 |
| Transpose Matrix (전치 행렬) (0) | 2021.02.15 |
| Delta Search (델타 탐색) (0) | 2021.02.15 |